저는 수학을 접하고 배우면서 고대 사람들에게도 수학은 있었을까?
그들은 수를 어떻게 인식하고 일상생활에서 사용했을까? 숫자는 언제부터 사용했을까? 등의
여러 질문을 하게 되었습니다. 그러면서 고대 사람들의 수학에 대해 탐구해 보게 되었는데요.
오늘은 이집트 문명에서 어떻게 수학이 만들어졌고 발생했는지 알아보면 좋겠습니다.
고대 이집트 문명은 나일강을 따라 형성되었습니다. 이집트 절대왕권의 상징인 피라미드에는 수학적인 비밀이 숨겨져 있습니다. 기술력이 뛰어나지 않았던 고대에서 어떻게 큰 피라미드를 만들었을까요?
농경사회와 피라미드
고대 이집트는 기원전 4000년경부터 농업을 시작하였고, 일찍부터 농업국가로 발전했습니다. 그들에게 땅은 무척 중요했기 때문에 토지를 균등하게 분배하는 일은 아주 큰 관심사였습니다. 이집트를 다스리는 왕인 파라오는 토지를 어떻게 하면 균등하게 나눌 수 있을까 고민을 했어야 했죠. 그래서 분배수학이 발전하기 시작했습니다.
또한 나일강이 많이 범람했었는데 토지의 경계선을 복구하기 위해 측량술과 기하학이 발달하기 시작하였습니다. 기하학(geometry)은 geo(땅)과 merty(측량하다)를 합친 단어로 토지를 측량하며 발전한 학문이라고 볼 수 있습니다. 그 당시 이집트인들은 이집트를 다스리는 왕인 파라오가 죽으면 나일강의 신으로 부활해서 홍수를 조절하면서 풍년을 가져온다고 믿었습니다. 이러한 영혼불멸사상을 믿었기 때문에 파라오는 직위 하자마자 자신의 무덤이 되는 피라미드를 건축하기 시작하였습니다. 가장 대표적인 쿠푸왕의 피라미드는 기원전 2560년에 2.5톤의 돌을 230만 개를 쌓아 만들었습니다. 2분에 1개씩 돌을 옮겼다고 가정했을 때 2~3만 명의 사람이 하루에 340개씩 옮겨 23년이 걸렸다는 수치가 나오고 있습니다.
피라미드에 숨겨진 수학적인 4가지 비밀
1. 정확한 정사각형의 밑변: 정확히 정사각형으로 측량되지 않는다면 건축물은 불안하고 흔들리게 됩니다.
2. 52도의 경사각: 자연환경이 만들어지는 각도가 52도였는데 이집트인들은 이것을 이용했습니다.
3. 밑변, 높이, 빗변의 길이들로 피타고라스의 정리가 성립됩니다. 황금비율의 이차방정식을 구할 수 있습니다.
4. 피라미드의 높이를 구의 반지름으로 본다면 피라미드 밑면의 둘레와 구의 둘레가 같게 됩니다.
숫자와 파피루스
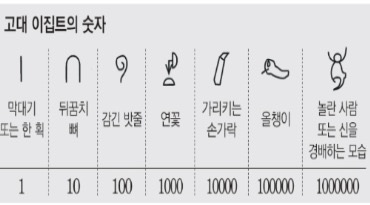
인간은 수를 인식할 때 ‘1:1 대응’을 가지고 인식하였습니다. 자신의 동물이 몇 마리인지 셀 때 돌멩이와 동물을 대응시켜 돌멩이의 숫자를 세거나 막대기를 긋는 행위를 하였습니다. 대응을 통해 수의 개념을 만들어내었고, 손가락 10개를 보면서 십진법을 만들었습니다. 그들은 숫자를 만들 때 문화와 자연과 밀접한 사물 모양으로 나타냈습니다. 1은 막대기 모양으로 나타냈고, 10은 막대기가 구부러진 모양(뒤꿈치 뼈)으로 나타냈습니다. 100은 감긴 밧줄, 1000은 연꽃, 10000은 손가락(또는 파피루스의 싹), 10만은 올챙이, 100만은 놀란 사람의 모양 (또는 신을 경배하는 모습)으로 표현하였습니다. 그들은 벌써 100만이라는 수를 사용했는데 이는 거대 제국이었음을 나타내기도 합니다.
이 숫자들을 어디에 기록했을까요? 이집트 식물인 파피루스로 종이를 만들었고 그 종이에다 글을 썼습니다. 글을 읽을 수 있는 사람들은 오직 1%뿐이었습니다. 특출 난 사람이나 계급이 높은 자들이었는데 특히 서기관이라는 학자들이 파피루스를 이용하여 많은 기록을 했다고 합니다. 파피루스 갈대를 태우면 검은 재가 나오는데 다른 성분과 섞어 잉크를 만들어 기록했습니다. 이러한 필기구나 종이의 발전 또한 수학의 발전에 많은 영향을 미쳤습니다. 파피루스의 단점은 불에 타면 빠르게 소멸되는 것이었습니다.

또한 그들의 주식은 맥주와 빵이었는데, 빵을 나누어 먹는 문제로 인해 분배수학, 분수가 발달할 수 있었습니다. 예를 들어 9개의 빵을 10명에게 동등하게 나누는 방법이 무엇일까? 와 같은 실생활 문제를 많이 접했을 것입니다. 이러한 식생활 문제로 인해 수학적인 사고를 하였고, 어려가지 수학적인 문제들이 발전하기 시작했습니다.
출처 | 이야기수학사
'온유쌤의 수학 노트 > 수학사와 수학자' 카테고리의 다른 글
| [수학자] 탈레스(Thales)_ 논증 기하학, 철학의 아버지 (0) | 2023.02.10 |
|---|---|
| [수학사] 고대 그리스 수학_아테네와 수학자들 (0) | 2023.02.10 |
| [수학사] 숫자의 발달_ 중국의 숫자와 수의 확장 (0) | 2023.02.09 |
| [수학사] 숫자의 발달_ 아라비아 숫자와 인도 수학 (0) | 2023.02.07 |
| [수학사] 고대 메소포타미아의 수학_루트2와 60진법 (0) | 2023.02.07 |




댓글